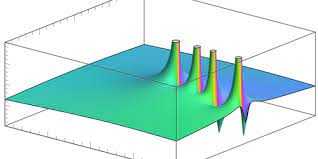
Fonction Riemann Zeta

Fonction Riemann Zeta, fonction utile dans la théorie des nombres pour étudier les propriétés des nombres premiers. Écrit comme ζ (x), il a été initialement défini comme la série infinie ζ (x) = 1 + 2^-X + 3^-X + 4^-X + ⋯. Lorsque x = 1, cette série est appelée la série harmonique, qui augmente sans liée - je.e., sa somme est infinie.

1. Quelle est la fonction Riemann Zeta utilisée pour?
2. Comment calculer la fonction Riemann Zeta?
3. Qui a résolu la fonction Riemann Zeta?
4. La fonction Riemann Zeta a-t-elle été résolue?

Quelle est la fonction Riemann Zeta utilisée pour?

La fonction Riemann Zeta code pour les informations sur les nombres premiers - les atomes de l'arithmétique et essentiels à la cryptographie moderne sur laquelle le commerce électronique est construit. Trouver une preuve a été le Saint Graal de la théorie des nombres depuis que Riemann a publié pour la première fois son hypothèse.

Comment calculer la fonction Riemann Zeta?

\ zeta (s) = \ sum_ n = 1 ^ \ infty \ dfrac 1 n ^ s. ζ (s) = n = 1∑∞ ns1. Il est ensuite défini par la continuation analytique d'une fonction méromorphe sur l'ensemble c \ mathbb c c par une équation fonctionnelle.

Qui a résolu la fonction Riemann Zeta?

Les valeurs de la fonction Riemann Zeta à des entiers même positives ont été calculées par Euler. Le premier d'entre eux, ζ (2), fournit une solution au problème de Bâle. En 1979, Roger Apéry a prouvé l'irrationalité de ζ (3).

La fonction Riemann Zeta a-t-elle été résolue?

L'hypothèse de Riemann, une formule liée à la distribution des nombres premiers, est restée non résolue depuis plus d'un siècle.